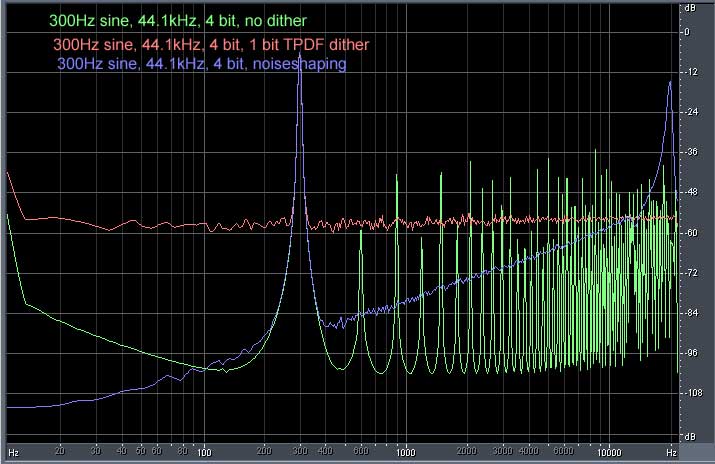
 |
| Spectral cleanup with dither |
There are a number of things that will affect the sound quality and the need for more bits and more samples. The modern CD loudness wars, which compress, limit and clip the audio into a quivering mass of Velveeta would get by with 8 bits and practically nobody would notice. A well-mastered and well-engineered CD at 16 bits and 44.1 KHz sample rate can sound fantastic. A poorly-mastered and poorly-engineered one will sound like crap.
Are there ever times when more than 16 bits and 44.1 KHz sampling would be better? Yes. In a recording environment, where the incoming live sound is unpredictable, it's better to leave some headroom for unexpected, accidental peaks. If you're using all 16 bits, and a louder peak comes along, it will overload the A/D converter. Eight additional bits provide 48 dB of additional headroom, which is itself more than the dynamic range of the vast majority of commercial CDs being sold today - especially the loudness war victims.
In addition, when mixing tracks, each additional track adds about 6 dB to the sum (assuming each track is mixed at full scale - a worst-case scenario). Mixing eight tracks will consume all 8 additional bits of headroom. To avoid overload, recording additional tracks means the level of all tracks will have to be attenuated in the mix. If they're 24 bit tracks, they can be turned down without any loss of resolution (they do have to be re-dithered however - in fact, audio should always be re-dithered when it is re-scaled - up or down).
For live recording and mixing, you can do better with 24 or even 32 bits (Audacity uses 32-bit floating point by default). But for commercial distribution via e.g., CD, 16 bits really is enough. Trust me on this.
So, what about sample rate? Well, that's much less important with modern oversampling sigma-delta A/D and D/A converters. Humans can hear at best, out to 20 KHz. Most of us are lucky if we can hear 15 or 16 KHz, although it really depends on how loud the signal is. I suspect more humans could hear 20 KHz if it's loud enough. For music, there just isn't much significant energy above 15 KHz. A sample rate of 44.1 KHz means that the digital recording system can accurately capture up to a maximum of 22.05 KHz: more than most anyone can possibly hear in a musical setting. The Nyquist Shannon sampling theorem tells us that we absolutely, positively need not sample more than twice the highest frequency of interest. This is not speculation; it is one of the most well-validated results in the field of information theory.
 |
| Aliasing |
In order to prevent ultrasonic frequencies, above 22.05 KHz, from getting into the A/D converter and getting aliased back down into the audio frequencies, the input should ideally be filtered. As a practical matter, the filtering requirement on A/D converters is fairly weak, because most music doesn't contain a lot of energy at or above 20 KHz, and certainly not far enough above to be aliased down to frequencies that we hear readily. Still, most good A/D converters do provide high quality "brick wall" anti-aliasing filters. It is very difficult to build analog brick wall filters, but modern (i.e., since about 1995) oversampling sigma-delta converters can do this using digital filters with mathematical precision. They hypersample internally, but they output e.g., 44.1 KHz or whatever the desired sample rate is.
The filter function is different for D/A converters, but the requirements are about the same. The output filters are used to remove the ultrasonic sidebands that are generated by the sampling process. Although we can't hear them, those ultrasonic frequencies can wreak havoc with amplifiers and tweeters, and they need to be removed. It is probably sufficient to merely attenuate the ultrasonic sidebands with a softer roll-off that won't over stress downstream equipment. But modern (i.e., since about 1995) oversampling sigma-delta converters can provide digital "brick wall" reconstruction filters with mathematical precision.
Back when ADCs and DACs ran at the nominal sample rate, we had to filter using analog elliptical filters, and I could justify a bit of "slack" between the stop band and the sample frequency. It reduced the constraints on the analog filter, which were critical and hard to keep in spec. In those days, sample rates of 48 or 50 KHz were common. But for today's oversampling sigma-delta ADCs and DACs with their built-in digital filters, any sample rate above 44.1 KHz is simply an outdated concept.
Do we need to sample at 96 KHz? Certainly not! It doesn't make the filtering job any easier. All you're adding is more load on the CPU and wasting storage space. If you can't hear 20 KHz, you're never going to hear 48 KHz, or anything in between. And 192 KHz? That's four times higher than 44.1 KHz! If you can't hear 20 KHz, neither you or your dog are going to hear 96 KHz. Why on earth store all that inaudible chaff? It's processor abuse!
